Welcome to the comprehensive system of linear inequalities worksheet, your ultimate guide to understanding and solving these essential mathematical concepts. In this interactive resource, we will delve into the world of linear inequalities, exploring their types, graphing techniques, and practical applications.
Linear inequalities are mathematical expressions that represent relationships between variables, providing valuable insights into real-world scenarios. This worksheet will equip you with the knowledge and skills to solve complex systems of linear inequalities, empowering you to make informed decisions and solve problems in various fields.
1. Defining System of Linear Inequalities
A system of linear inequalities is a set of two or more linear inequalities that are considered simultaneously.
Linear inequalities are mathematical statements that compare two linear expressions using the inequality symbols <, >, ≤, or ≥. Linear expressions are algebraic expressions that consist of variables and constants, combined using the operations of addition, subtraction, multiplication, and division.
Types of Linear Inequalities
- One-variable linear inequalities:These inequalities involve only one variable and have the form ax + b < c, ax + b > c, ax + b ≤ c, or ax + b ≥ c, where a, b, and c are constants and a ≠ 0.
- Two-variable linear inequalities:These inequalities involve two variables and have the form ax + by < c, ax + by > c, ax + by ≤ c, or ax + by ≥ c, where a, b, and c are constants and a and b are not both zero.
Examples of Linear Inequalities
- x + 2 < 5
- y – 3 ≥ 1
- 2x + 3y < 6
- 5x – 2y ≥ 10
2. Graphing Linear Inequalities

Graphing linear inequalities involves representing the solutions of the inequality on a coordinate plane.
Steps for Graphing Linear Inequalities, System of linear inequalities worksheet
- Graph the boundary line:Find the equation of the boundary line by replacing the inequality symbol with an equality sign. Plot the line on the coordinate plane using the slope-intercept form (y = mx + b).
- Determine the shading region:Determine which side of the boundary line satisfies the inequality. Shade the region that satisfies the inequality.
Examples of Graphing Linear Inequalities
- Graph the inequality y > 2x + 1.
- Graph the inequality x – y ≤ 3.
- Graph the inequality 2x + 3y < 6.
- Graph the inequality 5x – 2y ≥ 10.
3. Solving Systems of Linear Inequalities: System Of Linear Inequalities Worksheet
Solving systems of linear inequalities involves finding the region in the coordinate plane that satisfies all the inequalities in the system.
Methods for Solving Systems of Linear Inequalities
- Graphing method:Graph each inequality in the system and shade the region that satisfies all the inequalities.
- Substitution method:Solve one inequality for one variable and substitute the expression into the other inequality. Solve the resulting inequality for the remaining variable.
- Elimination method:Multiply each inequality by a constant so that one variable is eliminated. Solve the resulting system of equations for the remaining variable.
Examples of Solving Systems of Linear Inequalities
- Solve the system of inequalities:
- x + y < 5
- x – y ≥ 1
- Solve the system of inequalities:
- 2x + 3y ≤ 6
- x – y ≥ 2
- Solve the system of inequalities:
- x + 2y > 4
- 2x – y ≤ 5
4. Applications of Systems of Linear Inequalities
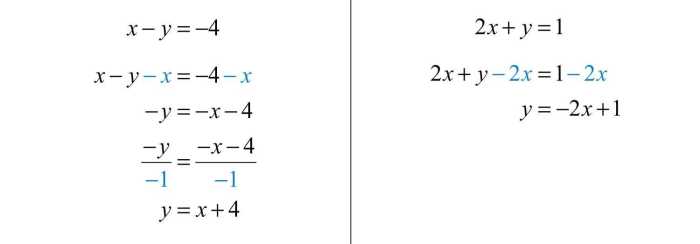
Systems of linear inequalities have numerous applications in various fields.
Real-World Examples
- Business:Optimizing production and distribution to maximize profits or minimize costs.
- Finance:Determining feasible investment portfolios that meet specific risk and return criteria.
- Engineering:Designing structures and systems that satisfy multiple constraints.
- Science:Modeling and predicting physical phenomena that involve multiple variables.
Importance of Systems of Linear Inequalities
- Decision-making:Systems of linear inequalities provide a framework for making informed decisions by identifying feasible solutions that meet multiple criteria.
- Optimization:They enable the optimization of processes and systems by finding the best possible solutions within a set of constraints.
- Modeling:Systems of linear inequalities can be used to model complex real-world situations and predict outcomes based on multiple factors.
FAQ Compilation
What is a system of linear inequalities?
A system of linear inequalities is a set of two or more linear inequalities that are connected by the word “and” or “or.”
How do I graph a system of linear inequalities?
To graph a system of linear inequalities, first graph each inequality individually. Then, shade the region that satisfies all of the inequalities.
How do I solve a system of linear inequalities?
To solve a system of linear inequalities, first graph the system. Then, find the region that satisfies all of the inequalities. The solution to the system is the set of all points in this region.

